...slip

slip is the deletion or repetition of bits due to a discrepancy in the read and write rates at a buffer.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...three

Strictly four. The standard has provisioned that SSU's in nodes which do and do not interface with customer equipment shall have different qualities although this is yet to be elaborated upon at the time of writing.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...Error

strictly Maximum Relative Time Interval Error (MRTIE) as it is only possible to measure one frequency relative to some reference.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...interest

the frequency range of interest is 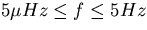$5\mu Hz\leq f\leq 5Hz$ which corresponds to observation intervals of 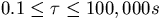$0.1\leq\tau\leq100,000s$. Since wander frequencies above 5Hz are rejected by clocks because of the low pass filtering of input noise inherent in phaselock loops, a high frequency cut-off of 5Hz is appropriate

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...filter

although it will be shown in section 5.2 that the model has assumed F(s)=1.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...ensemble

an ergodic ensemble is a set of functions which yield an identical statistical description when examined together to any one of the ensemble examined over a long period of time, i.e. the time and ensemble averages are identical.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...x

In actual fact the author took the expression in terms of x and worked backwards in order to demonstrate the high-pass filtering characteristic.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...outputs

assuming that noise sources from different clocks are uncorrelated

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...[4]

at the time of writing, part 5 is still out for consultation but it is expected that the value K_f=2977 from [14] will be adopted.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...obtained

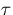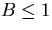
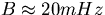
although the approximation derived for small $\tau$ is only valid for $B\leq 1$

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...$B\approx20mHz$

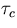
the results also confirm the expression (6.16) for $\tau_c$

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.