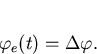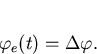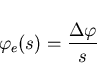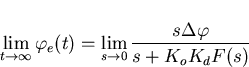Tracking phase steps

Consider the steady-state error resulting from a change of input phase of magnitude

$$\varphi_e(t)=\Delta\varphi.$$

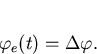
so that by taking Laplace Transforms

$$\varphi_e(s)=\frac{\Delta\varphi}{s}$$

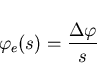
Substituting the above equation into equation (3.18) and then using the final value theorem (3.19) gives

$$\lim_{t\to\infty}\varphi_e(t)=\lim_{s\to0}\frac{s\Delta\varphi}{s+K_oK_dF(s)}$$

so for F(0)>0,

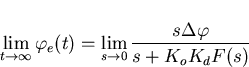
$$\lim_{t\to\infty}\varphi_e(t)=0.$$

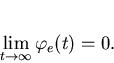
Therefore there is no steady-state phase error due to phase steps at the input. In other words, a phaselock loop will eventually track out any change in phase.