In practice it is almost always the case that the input signal never exactly agrees with the frequency of the VCO when no control voltage is applied (the free running voltage). In order to analyse this case it is necessary to consider the effect of a change of frequency at the input. Let such a frequency step have magnitude ![]() . Now it has been found [11] that in such cases
. Now it has been found [11] that in such cases
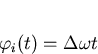
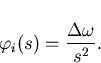
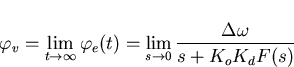
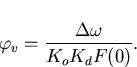 |
(24) |