



Next: Classification of Noise Types
Up: Frequency Metrology Measures
Previous: Basic Definitions
Since much subsequent discussion involves the analysis and modelling of phase noise it is appropriate to examine the relationship between phase and frequency fluctuations. For this reason, an expression for the fractional frequency deviation will be obtained. This will allow a relationship between fractional frequency error and time error to be derived.
Since
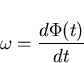
where 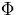 is the total phase of the signal produced by a non-ideal clock as defined in equation (3.1),
the frequency of the clock is
is the total phase of the signal produced by a non-ideal clock as defined in equation (3.1),
the frequency of the clock is
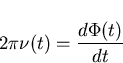
Substituting (3.1) the above equation becomes
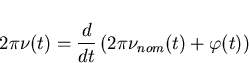
which upon simplifying and re-arranging becomes
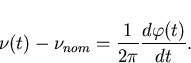
Dividing by 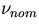 throughout, the expression
throughout, the expression
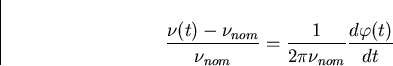
is obtained.
Substituting equation (3.3) yields the expression
| 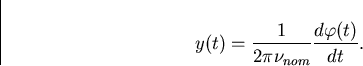 |
(8) |
Now by equation (3.2)
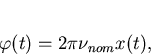
so substituting the above into (3.4) one obtains the following simple differential relationship between the fractional frequency deviation and time error of a clock
| 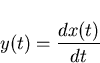 |
(9) |
Since it is impossible to measure instantaneous frequency, any frequency measure will involve a measurement interval 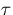 . In effect, in order to measure a fractional frequency, the time error is measured at time
. In effect, in order to measure a fractional frequency, the time error is measured at time 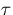 and subsequently at time
and subsequently at time 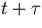 . From equation (3.5), the difference in these time errors divided by
. From equation (3.5), the difference in these time errors divided by 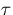 gives the average fractional frequency deviation over that period
gives the average fractional frequency deviation over that period 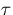 :
:
| 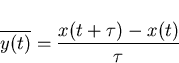 |
(10) |
Since it is not possible to have continuous knowledge of x(t). x is in practice a series of discrete samples 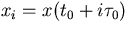 .
.




Next: Classification of Noise Types
Up: Frequency Metrology Measures
Previous: Basic Definitions
Mark J Ivens
11/13/1997
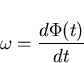
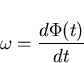
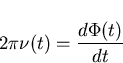
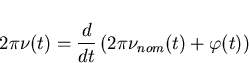
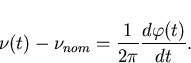
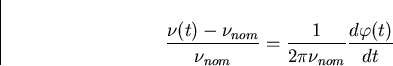
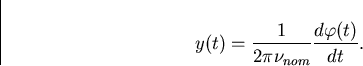
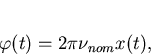
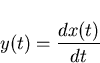
![]() . In effect, in order to measure a fractional frequency, the time error is measured at time
. In effect, in order to measure a fractional frequency, the time error is measured at time ![]() and subsequently at time
and subsequently at time ![]() . From equation (3.5), the difference in these time errors divided by
. From equation (3.5), the difference in these time errors divided by ![]() gives the average fractional frequency deviation over that period
gives the average fractional frequency deviation over that period ![]() :
:
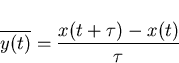
![]() .
.