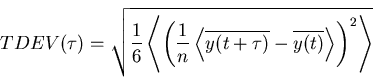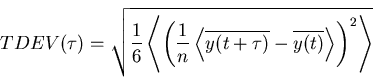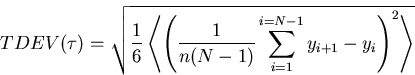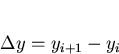TDEV as a function of fractional frequency error

TDEV can be expressed in terms of the fractional frequency deviation by  

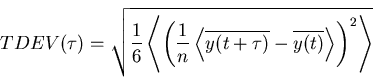$$TDEV(\tau)=\sqrt{\frac{1}{6}\left<\left(\frac{1}{n}\left<\overline{y(t+\tau)}-\overline{y(t)}\right\gt\right)^2\right\gt}$$ (26)

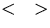where $<\quad \gt$ represents an infinite time average. For a set of N discrete samples y_i this may be estimated by  

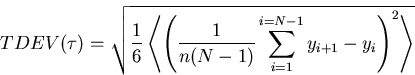$$TDEV(\tau)=\sqrt{\frac{1}{6}\left<\left(\frac{1}{n(N-1)}\sum_{i=1}^{i=N-1}y_{i+1}-y_{i}\right)^2\right\gt}$$ (27)

This expression gives some insight into the process that the TDEV expression is performing. The process central to the argument is the adoption of the measure

$$\Delta y=y_{i+1}-y_i$$

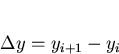
rather than 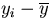$y_i -\overline{y}$ inherent in the conventional standard deviation. It is reported [24] that taking the set of 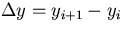$\Delta y=y_{i+1}-y_i$ is equivalent to high pass filtering the data. Thus performing such a process removes the drift from the signal in figure 4.1 so that it becomes as shown in figure 4.2.

 

Figure 4.2:   Noise signal with drift removed by high-pass filtering

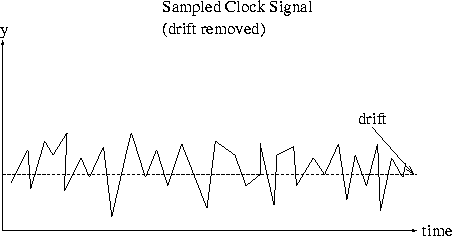This signal would converge. Note that the TDEV filtering characteristic is again discussed in section 4.1.5.