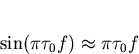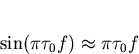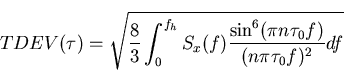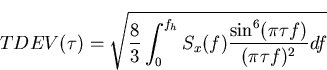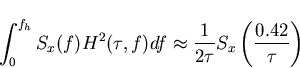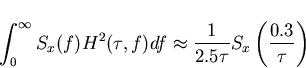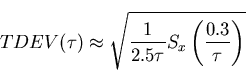An approximate expression for TDEV illustrating its filtering behaviour

 A useful approximation to make equation (4.6) more analytically tractable has been obtained by Dan Wolaver of Tektronix Ltd.[19]. For 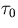$\tau_0$ small to avoid anti-aliasing,

$$\sin(\pi \tau_0 f)\approx \pi \tau_0 f$$

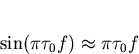
over the range of integration 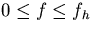$0\leq f \leq f_h$.Thus equation (4.6) becomes

$$TDEV(\tau) = \sqrt{\frac{8}{3}\int_{0}^{f_h}S_x(f)\frac{\sin^{6}(\pi n \tau_0 f)}{(n \pi \tau_0 f)^2}df}$$

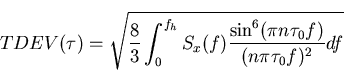
which since 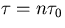$\tau=n\tau_0$, simplifies to

$$TDEV(\tau)=\sqrt{\frac{8}{3}\int_{0}^{f_h}S_x(f)\frac{\sin^{6}(\pi\tau f)}{(\pi \tau f)^2}df}$$

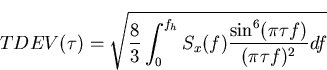
Thus TDEV may be approximated by

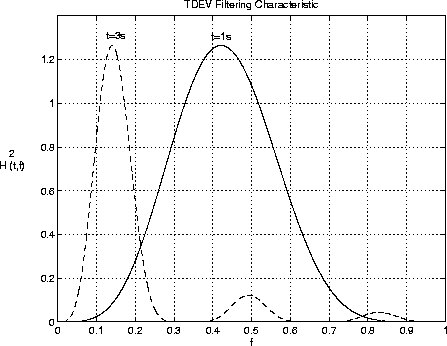
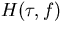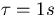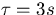From the above equation, TDEV is the rms of phase filtered by $H(\tau,f)$. This function is plotted in figure 4.3 for $\tau=1s$ and $\tau=3s$. It can be seen 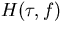$H(\tau,f)$ is nearly zero except near 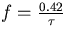$f=\frac{0.42}{\tau}$ and that the filter can be loosely approximated to a bandpass filter centred on $\frac{0.42}{\tau}$.

 

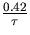Figure 4.3:   Frequency Response of TDEV Filter for 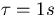$\tau=1s$ and $\tau=3s$

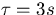
Since the area under the curve is 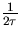$\frac{1}{2\tau}$, one might use the approximation

$$\int_{0}^{f_h}S_x(f)H^2(\tau,f)df\approx\frac{1}{2\tau}S_x\left(\frac{0.42}{\tau}\right)$$

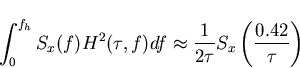
In actual fact, the bandpass is very wide and because dominant noise sources such as flicker phase (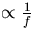$\propto \frac{1}{f}$) etc. have strongest spectral components at low frequencies, the approximation

$$\int_{0}^{\infty}S_x(f)H^2(\tau,f)df\approx\frac{1}{2.5\tau}S_x\left(\frac{0.3}{\tau}\right)$$

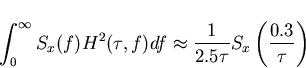
is more appropriate and has been found [20] to be within 20% of the exact value for observation intervals up to 10⁶ seconds. Thus TDEV may be approximated by  

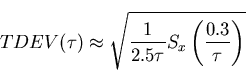$$TDEV(\tau)\approx\sqrt{\frac{1}{2.5\tau}S_x\left(\frac{0.3}{\tau}\right)}$$ (31)