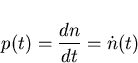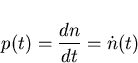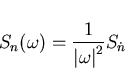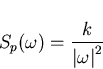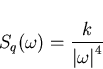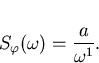Flicker Phase Noise Shaping of Filter A

It can easily seen that Filter A performs flicker phase noise spectral shaping. Consider a white gaussian noise source with power spectral density $S_{WGN}(f)=\frac{1}{2} \eta$ where $\eta$ is a constant. The PSD of the noise signal once it has passed through a filter with transfer function H(f) can be found using the relation (5.2)

S_out(f)=|H(f)|²S_in(f).

Thus a white Gaussian noise source input into Filter A with transfer function (2.2) will clearly produce an output signal with power spectral density 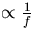$\propto \frac{1}{f}$ which is flicker phase noise. The following argument due to Barnes and Allan [15] demonstrates the rationale behind the flicker phase noise spectral shaping property of an 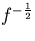$f^{-\frac{1}{2}}$ filter. 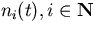Consider an ergodic ensemble of functions $n_i(t), i\in \mathbf{N}$ generating white phase noise with a zero ensemble average so that

where k is a constant. where k is a constant. Now consider

$$p(t)=\frac{dn}{dt}=\dot{n}(t)$$

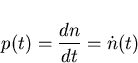
Using the well known relation (3.8)[16]

$$S_n(\omega)=\frac{1}{\left\vert\omega\right\vert^2}S_{\dot{n}}$$

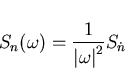
it is evident that

$$S_p(\omega)=\frac{k}{\left\vert\omega\right\vert^2}$$

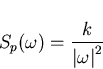
Similarly, if 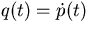$q(t)=\dot{p}(t)$then

$$S_q(\omega)=\frac{k}{\left\vert\omega\right\vert^4}$$

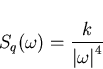
It can be seen that each time the function n(t) is integrated, a factor 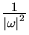$\frac{1}{\left\vert\omega\right\vert^2}$ is applied to the phase power spectral density. From the discussion in section 3.2, flicker phase modulation is of the form

$$S_{\varphi}(\omega)=\frac{a}{\omega^1}.$$

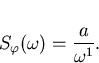
where a is a constant. Thus it can be seen that flicker phase noise is equivalent to a gaussian white noise source shaped by a 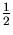$\frac{1}{2}$ order integrator.