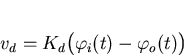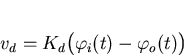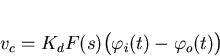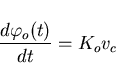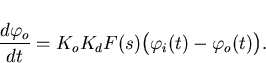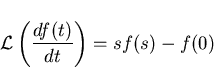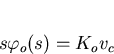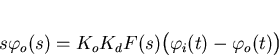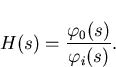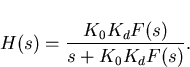Analysis of basic PLL Function

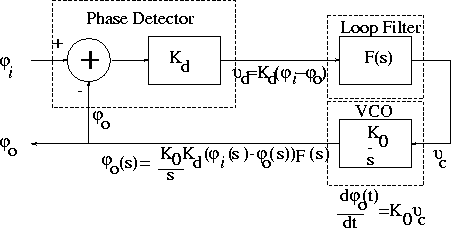
 In this section elementary mathematical analysis of a simple phaselock loop is performed in order to obtain the phaselock loop transfer function. The basic phaselock loop components are shown again in figure 3.2. Further to the discussion in section 3.4.1, the function of a phase detector is to produce an output voltage proportional to difference in phase between its inputs. Thus the phase detector output voltage, v_d is given by

$$v_d=K_d\big(\varphi_i(t)-\varphi_o(t)\big)$$

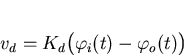
where K_d is the phase-detector gain factor measured in volts/radian. The phase detector output voltage v_d then passes through the loop filter. The voltage at the output of the loop filter is given by

v_c=v_dF(s)

i.e.

$$v_c=K_dF(s)\big(\varphi_i(t)-\varphi_o(t)\big)$$

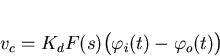
The deviation of the VCO from its centre frequency is given by  

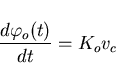$$\frac{d\varphi_o(t)}{dt}=K_ov_c$$ (15)

where K_o is the VCO gain factor which has units rad/sec-V. Substituting for v_c yields

$$\frac{d\varphi_o}{dt}=K_oK_dF(s)\big(\varphi_i(t)-\varphi_o(t)\big).$$

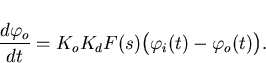
Taking the Laplace transform on both sides of (3.11) and using

$$\mathcal{L}\left(\frac{df(t)}{dt}\right)=sf(s)-f(0)$$

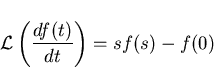
gives

$$s\varphi_o(s)=K_ov_c$$

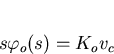
which on substituting for v_c becomes  

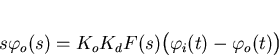$$s\varphi_o(s)=K_oK_dF(s)\big(\varphi_i(t)-\varphi_o(t)\big)$$ (16)

Equation (3.12) may be easily rearranged to obtain the closed loop transfer function

$$H(s)=\frac{\varphi_0(s)}{\varphi_i(s)}.$$

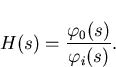
Performing such a manipulation yields the expression  

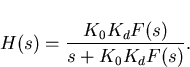$$H(s)=\frac{K_0 K_d F(s)}{s+K_0 K_d F(s)}.$$ (17)

It can be seen from the form of the equation that PLL's essentially low pass filter incoming signals.

 

Figure 3.2:   PLL block schematic